统计基础-区间估计

如果我们想知道一所办公楼的所有人员的平均身高，该怎么做？大家应该都能想到，我们可以通过统计抽样的办法，随机去调查一些人的身高，然后通过这些人的平均身高去估计所有人员的平均身高。但这里还有一个问题，这里抽样得到的平均身高准吗？有多准呢？

要回答这里的问题，我们需要有一些基本的统计学知识。

下面以简单的掷硬币的例子来说明一下。我们知道掷一次硬币，得到正面向上和反面向上的概率都是50%。用X表示这里的随机事件，用0表示正面向上，用1表示反面向上。我们可以得到X=k的分布，即

$P(X=k) = 0.5, k=0,1$

上面的问题是离散型随机变量的分布问题。我们最开始的身高的例子则是一个连续型的随机变量分布问题。对于一个连续型的随机变量，大家最熟悉的分布就是正态分布了。比如，人的身高我们可以认为服从一个均值为μ，方差为σ^2的正态分布。但人的身高分布就没法简单的用某一个值的概率来表示了，因为此时的概率都为0.为了描述人的身高的分布，我们会用概率密度函数来描述。由正态分布的定义可以知道，身高的概率密度函数为：

$f(x) = {1 \over \sqrt{2\pi}\sigma}e^{-{(x-\mu)^2 \over 2\sigma^2}}, x \in (0,+\infty)$

对应的分布函数，我们可以用概率密度函数的积分来表示。比如我们想知道有多大概率分布在1.7米到1.8米之间。那么此时的概率为：

$F(1.7 < x < 1.8) = \int_{1.7}^{1.8} f(x)dx$

以上是最基本的统计学知识，高中课本就有学习，带大家复习一下。

想解决最开始的身高估计有多准确的问题，我们还得更进一步。考察一下做n次掷硬币试验，或者抽样n个人的情况。

我们先来看n次掷硬币试验的问题。一般而言，由于硬币的铸造误差，使得正面向上和反面向上的概率不会严格相等。那么，通过掷硬币n次，我们能不能判断硬币正面向上和反面向上的概率是否相等呢？这个的问题其实与文章最开始的问题是类似的，这里我们假设掷硬币正面向上的概率未知，开始的题目假设平均身高未知，然后都试图通过一定次数的试验来了解这些未知的量。

为了回答上述问题，我们先来考虑一下下面这个问题。对于这个n次掷硬币的大试验，假设我们重复做了m次，即投掷硬币m * n次，每次大试验都可以得到一个正面朝上的次数。假设n为100，这里得到的次数可能是[50, 49, 44, 52, ...]，也就是说这枚硬币正面朝上的估计概率为[0.50, 0.49, 0.44, 0.52, ...]。这些数据实际上可以构成另一个随机变量取值序列。这个高阶随机变量是不是会服从一个什么分布呢？事实上，由中心极限定理可知，这里的高阶随机变量将服从一个正态分布，其均值和方差分别为p和p(1-p)/n，其中p为真实的硬币正面朝上的概率。

这里我们居然将离散的随机变量与描述连续的正态分布给联系上了，不得不感叹数字的奇妙！

有了这个正态分布，我们就可以做一些事情了。既然是正态分布，那么取值（当进行一次n次掷硬币的大试验时，得到的硬币正面朝上的估计概率）落在正态分布的两边的概率就会比较小。具体来说，一次试验的取值大约有95%的概率会落在距离均值的两个标准差(下图非阴影区域)之内。

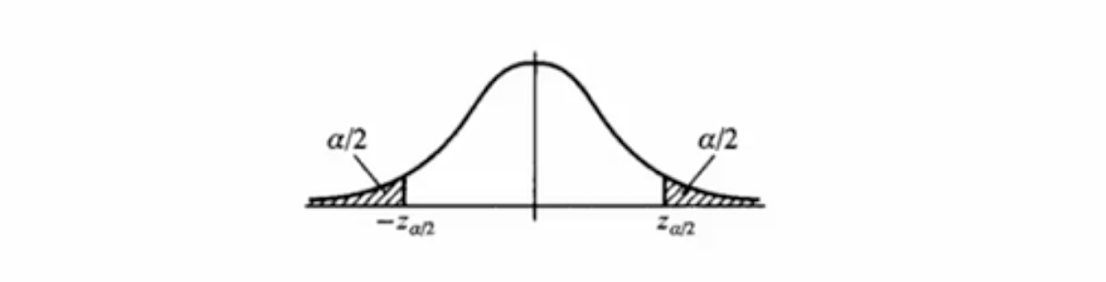
转换一个说法，假设这个取值为p_，我们考察均值p与样本值p_的距离，则

$P(|p - p\_| < 2 * {\sqrt{p * (1 - p) \over n}}) = 0.95$

即，我们可以有95%的把握可以认为，区间

$(p\_ - 2 * {\sqrt{p * (1 - p) \over n}},\enspace p\_ + 2 * {\sqrt{p * (1 - p) \over n}})$

将包含真正的p值。由于我们当前还不知道真实的p值，可以用p_来替代p进行近似计算。

我们似乎已经可以回答前面的问题了。硬币正面向上和反面向上的概率是否相等呢？假设做完一次投掷100次硬币的试验之后，我们得到40次正面朝上，则我们有95%的把握可以认为区间(0.4 - 2 * sqrt(0.4 * (1 - 0.4) / 100), 0.4 + 2 * sqrt(0.4 * (1 - 0.4) / 100))即(0.302, 0.498)将包含真正的正面朝上的概率。可以看到，这个区间不包含0.5，所以，这个硬币正面向上和反面向上的概率应该是不相等的。但如果我们得到45次正面朝上，这时的区间将为(0.351, 0.549)，由于区间包含了0.5，我们就不能说正面向上和反面向上的概率不相等。

上述过程正是统计学中经典的区间估计的内容，有兴趣的小伙伴可以查阅其他资料继续深入研究一下。

有了上面的知识，我们可以将其迁移到身高的平均值问题上来。多次进行抽样试验得到的样本均值会服从什么样的分布呢？经过数学推导知道，可以在样本均值基础上构造一个t统计量，它将服从另一个分布，即t分布。具体来说，统计量(样本均值 - 总体均值) / (样本标准差 / sqrt(n))将服从分布t(n-1). t分布的数学形式比较复杂，这里就暂时不介绍了，一般我们可以通过python代码取得其分布的值。t分布的概率密度函数曲线如下：

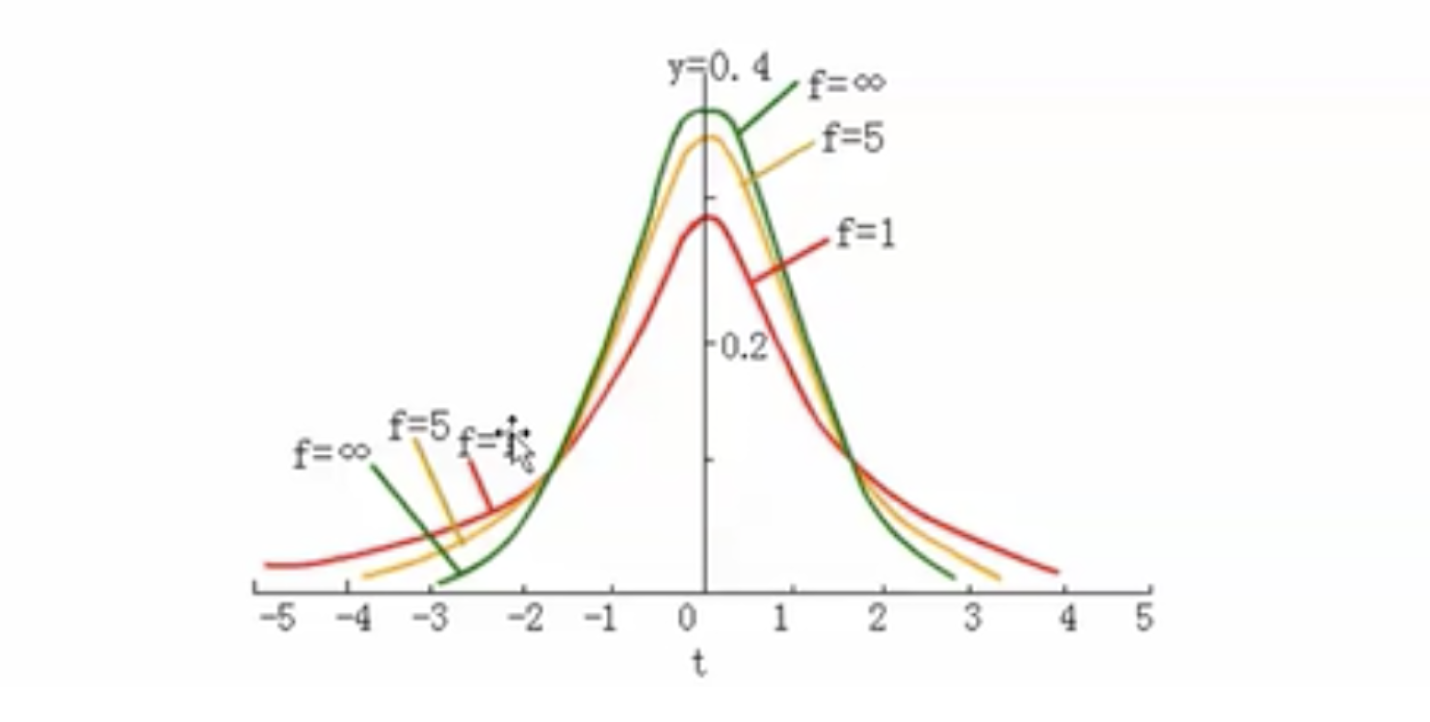
上图中有很多条曲线，究竟是哪条曲线由n的取值来确定。

采用与前面类似的思想，做一次试验得到的值落在t分布的两边的概率是比较低的。假设我们以95%的把握来看这个问题，则

$0.95 = P(|{\bar{x} - \mu \over S / \sqrt{n}}| < t_{\alpha/2,n-1}) = P(\bar{x} - t_{\alpha/2,n-1} * {S \over \sqrt{n}} < \mu < \bar{x} + t_{\alpha/2,n-1} * {S \over \sqrt{n}}) \\ \text{其中：}\bar{x}\text{为样本均值， }\mu\text{为总体均值， }S\text{为样本标准差， }n\text{为试验次数}$

这样我们就得到了总体均值μ的估计区间了。

下面我们举例计算一下。假设，抽样得到的身高为[1.7, 1.6, 1.8, 1.72, 1.75, 1.74]，则：

$\text{样本均值}\enspace\bar{x} = {1.7 + 1.6 + 1.8 + 1.72 + 1.75 + 1.74 \over 6} = 1.72 \\ n = 6,\enspace n-1 = 5 \\ \text{95\%的置信度时}\enspace \alpha = 0.05,\enspace t_{\alpha/2, 5} = 2.571 \\ s = \sqrt{(1.7 - 1.72)^2 + (1.6 - 1.72)^2 + (1.8 - 1.72)^2 + (1.72 - 1.72)^2 + (1.75 - 1.72)^2 + (1.74 - 1.72)^2 \over 5} = 0.0612 \\ \text{总体均值估计区间为：}\enspace(\bar{x} - t_{\alpha/2,n-1} * {S \over \sqrt{n}}, \bar{x} + t_{\alpha/2,n-1} * {S \over \sqrt{n}}) = (1.650, 1.790)$

即，我们可以有95%的把握认为区间(1.650, 1.790)包含了真正的平均身高。

回到我们的主题，抽样得到的平均身高准吗？除了可以说平均身高大约为1.72，我们还可以给出一个区间(1.650, 1.790)，有95%的可能性真实均值会在这个区间之内。